Problem Set for Previewing Unit 3
In the third unit of Math I students
are beginning their understanding of proofs, properties of triangles, and
properties of quadrilaterals. In this
preview we will focus on some of the properties of triangles and some of the
points of concurrency that lie within.
The students need to be able to identify perpendicular bisectors,
medians, angle bisectors, and altitudes on a triangle; in addition, the points
of concurrency that occur within the triangle when looking at these 4 different
types of lines. We do not want to limit
the students understanding of a point of concurrency to only these four;
however, these are the only four which students will see in Math I.
Vocabulary
Triangle Perpendicular
Bisector Median Angle
Bisector Altitude Centroid Circumcenter Orthocenter Incenter
Background
Here are
some fun activities that can help students better understand the term center
of mass.
Investigation
From the Project Intermath Webpage, we are
going to be using the Balancing
the Triangular Teeter activity. Working with the class we will learn about
the 4 points of congruency created by the perpendicular bisector, median, angle
bisectors, and altitudes. To better
introduce the where these points intersect we can use a paper folding activity
found here
(starts on page 7). Here is how to fold the paper to create the circumcenter,
incenter
and centriod. In order to explore
the perpendicular bisector, median, angle bisector, and altitudes points of
concurrency we can use this. This Geogebra
file can help with showing students where the centers move depending on whether
we are given an acute, right, or obtuse triangle.
Properties
of Points of Concurrency
Circumcenter
1)
The circumcenter is equidistant to the vertices of the triangle
2)
The circumcenter is the center point of a circle that intersects
the three vertices of the triangle. This
is called circumscribing a triangle.
Incenter
1)
The incenter is equidistant to the sides of the triangle
2)
The incenter is the center of a circle that intersects the three
sides of the triangle only once. This is
called inscribing the circle.
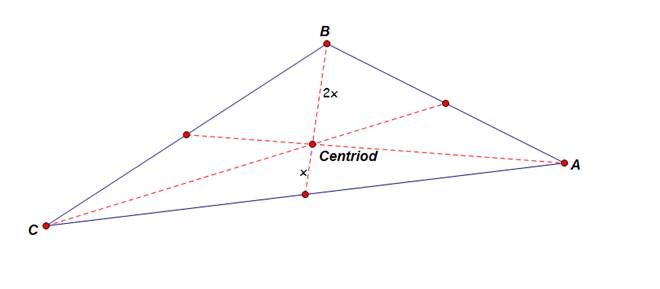
Centriod
1)
The centriod is also known as the center of balance for a
triangle.
2)
The distance from the vertex to the centriod is 2 times the
distance from the centriod to the side of the triangle